개념

심슨의 역설은 데이터의 상세 그룹에서 나타나는 평균, 추세 등과 이를 전체 그룹화 시켜서 평균, 추세 등을 비교 해보면 서로 상반되거나 다른 결론에 이룰 수 있다는 역설이다.
좀 더 간단하게 표현해 보자면

$$ a > b \\ c > d \\ a + c < b + d$$

이렇게 a, c의 각각(상세그룹)은 b, d 각각(상세그룹) 보다 크지만, a+c , b+d 합산(전체그룹) 크기를 비교 했을때 상반된 결과가 나올 수 있다는 의미이다.
이런 상황은 일상생활에서도 많이 나오는 것 이기도 하며 사례를 통해서 확인해보자.

사례 - 신장결석 치료법 [사례참고 : 위키피디아]

신장결석 치료법에 대한 설명 및 현상

• 아래의 표는 작은크기의 신장결석과 큰 크기의 신장결석에 대해 두 가지 치료법을 적용한 결과 성공율을 나타낸 표이다

  성공/실패	치료법 A	치료법B
  성공	78%(273/350)	83%(289/350)
  실패	22%(77/350)	17%(52/350)

  위 표에서는 치료법B가 신장결석 치료에 더 우수하다고 나온다. 하지만 위 데이터를 아래와 같이 결석크기에 따라 표를 세분화 해보면

  결석크기	성공/실패	치료법 A	치료법B
  작은결석	성공	93%(81/87)	87%(234/270)
  	실패	7%(6/87)	13%(36/270)
  큰결석	성공	73%(192/263)	69%(55/80)
  	실패	27%(71/263)	31%(25/80)

  상세그룹을 보게 되면 치료법 A가 작은/큰 결석 둘다 우수하다고 나온다는 것이 심슨의 역설현상 이다.

  위 내용을 개념 설명에서 사용했던 수식으로 나타내 보면

  \(\begin{eqnarray} P(성공|치료법A,작은결석) = 8/87=93\% 를 \quad a 라두고 \\ P(성공|치료법B,작은결석) = 234/270=87\% 를 \quad b 라두고 \\ P(성공|치료법A,큰결석) = 192/263=73\% 를 \quad c 라두고 \\ P(성공|치료법B,큰결석) = 55/80=69\% 를 \quad d 라두고 \\ P(성공|치료법A) = 273/350=78\% 를 \quad a + c 라두고 \\ P(성공|치료법B) = 289/350=83\% 를 \quad b + d 라두면 \end{eqnarray}\) \(\Rightarrow\) \(\begin{eqnarray} a (93\%) > b (87\%) \\ c (73\%)> d (69\%) \\ a + c (78\%) < b + d(83\%) \end{eqnarray}\)

  심슨의역설 현상이 나타남을 알 수 있다.

• 그럼 왜 부호가 바뀌었을까 ?

\[P(성공|치료법A) = P(성공|치료법A,작은결석)P(작은결석|치료법A) + P(성공|치료법A,큰결석)P(큰결석|치료법A)\] \[P(성공|치료법B) = P(성공|치료법B ,작은결석)P(작은결석|치료법B) + P(성공|치료법B ,큰결석)P(큰결석|치료법B)\]

이를 a, b의 표현으로 바꿔보면

\[a+c = a \times \color{Blue} {P(작은결석|치료법A)} + c \times \color{Blue} {P(큰결석|치료법A)}\] \[b+d = b \times \color{Blue} {P(작은결석|치료법B)} + d \times \color{Blue} {P(큰결석|치료법B)}\]

위 산식에서 파란색으로 표시된 가중치가 붙는것을 알 수 있다.

예제에서는 가중치는 치료법에 대한 결석의 종류이고 이 값에 따라서 부등호가 변경이 되며 심슨역설 현상이 나타나거나 나타나지 않을 수 있다는 것이다.

연속변수에서 심슨의 역설

• 범주형 자료 뿐만 아니라 심슨의 역설은 연속형 변수에서도 확인 할 수있다.

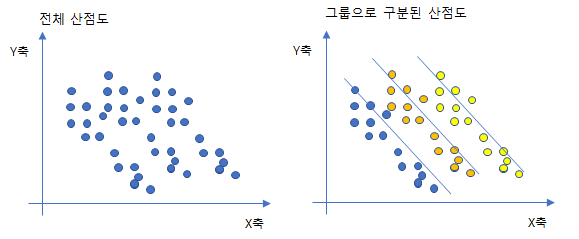
위 그림에서 전체 산점도는 X,Y가 관계없는 변수 같지만, 그룹으로 구분 시키면 역의 상관관계가 있음을 확인 할 수 있다.

결론

데이터를 분석하고 해석하는 경우 심슨의 역설에 주의를 기울어야 한다. 이 뿐만 아니라 통계에 있어 다른 지표들도 이러한 함정에 많이 노출 되어 있기 때문에 항상 유념 해서 해석 해야 할 것이다. 해결은 Data분석 이전에 해당 분야의 전문가들의 사전 지식이 필요하다.